在數學中,四凸是指一類既是凸的又是正的的四維多胞體。它們是正多面體和正多邊形的四維類比。它們最先在19世紀被數學家施萊夫利發現,其中五個與五個柏拉圖立體一一對應,另外一個沒有好的三維類比。
四維凸正多胞體
概述
在數學中,特別是在幾何和多面體幾何中,四維凸正多胞體被定義為在四維空間中具有以下特性的多胞體:


- 凸性:每兩個面的交線(邊)都是直線。
- 正性:所有的面都是相同形狀的正多面體,且所有邊和角都具有相等的長度和大小。
- 四維:這些多胞體是四維空間中的立體結構,而不是三維空間中的平面結構。
這些四維多胞體在19世紀被數學家路德維希·施萊夫利(Ludwig Schläfli)首次發現,並且與三維空間中的柏拉圖立體和二維空間中的正多邊形有類似的對應關係。在施萊夫利的系統中,五個四維凸正多胞體與五個三維空間中的柏拉圖立體一一對應,而第六個四維凸正多胞體(正二十四胞體)則沒有直接的三維類比。
特徵
| 名稱 | 描述 | 考克斯特羣 |
|---|---|---|
| 正八胞體(8-cell) | 由八個正方體胞面組成,對應於三維空間中的正方體。 | Cochrane羣,階為24 |
| 正二十胞體(20-cell) | 由二十個正四稜錐胞面組成,對應於三維空間中的正四面體。 | Alternating羣,階為120 |
| 正二十四胞體(24-cell) | 由二十四個正八面體胞面組成,沒有明顯的三維類比。 | Coxeter羣,階為192 |
| 正三十二胞體(32-cell) | 由三十二個正六邊形胞面組成,對應於三維空間中的正八面體。 | Coxeter羣,階為1152 |
| 正六十胞體(600-cell) | 由六百個正五邊形胞面組成,對應於三維空間中的正二十面體。 | Coxeter羣,階為14400 |
| 正七十二胞體(720-cell) | 由七百二十個正三角形胞面組成,對應於三維空間中的正十二面體。 | Coxeter羣,階為51840 |
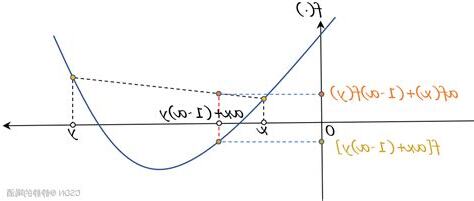
仿射函數
對於Rn上的仿射函數,當其定義在整個Rn空間上時,它們被認為是凸的且凹的。這是一個有用的定義,因為它允許我們將凸函數視為一個更大的集合中的特例,並且在推導和定義中可以簡化論證。然而,需要注意的是,這些仿射函數並不是本質上與凸函數相關的,而是作為一個工具來幫助我們理解和管理凸函數的性質。
凸函數的定義
如果epi f是Rn+1的凸子集,那麼我們將f定義為凸函數。相反地,如果負f為凸,則f是凹的。當集中在有效定義域上時,這些概念可以很容易地應用。然而,在本文中,我們選擇了一種方法,即考慮定義在整個Rn空間上的函數,即使它們可能取無窮大。這樣的話,對於xn不在S中的點,我們可以通過將f(xn)設為無窮大來擴展凸函數f。這種方法的好處是不用擔心有效定義域的問題,因為對於給定的形式,只要展示了f(xn)的具體值,就可以同時確定有效定義域。
四凸是指在遊戲中擁有四位角色皆達到極限突破的一種狀態。這種狀態通常代表玩家在遊戲中投入了大量的時間和精力,以達到最高的隊伍實力。
四凸的達成不僅需要收集各種珍稀素材,還需要解鎖角色的潛能,提升能力值和技能等級。這個過程往往需要通過完成困難的任務、參與戰鬥、以及持續的培養和訓練。
四凸擁有許多優勢,如更高的生命值、攻擊力、防禦力、技能傷害等等。同時,四凸還可以解鎖更強大的技能和特殊能力,使角色在戰鬥中更具威脅性。
然而,要達到四凸並不容易。它需要玩家有足夠的智慧和策略,以及耐心和毅力。而那些能夠達到四凸的玩家,往往也是遊戲中最強大的存在之一。
在遊戲社羣中,四凸往往是一個非常熱門的話題。玩家們會分享自己達到四凸的心得和策略,並互相鼓勵和交流。同時,四凸也是許多玩家的目標,他們會為此不斷努力和挑戰自己。
總而言之,四凸是遊戲中充滿挑戰和機會的一個目標。它代表著玩家的努力和決心,以及對遊戲的愛和熱情。無論是在遊戲中達到四凸,還是在現實生活中追求自己的目標,努力和堅持才是關鍵。
延伸閲讀…
四維凸正多胞體 – 維基百科
漫步凸分析四——凸函數翻譯
