「正八面體展開圖」是一種八面體的視覺表徵,由八個等邊三角形和一個正方形組成的正方錐體。它是五種正多面體之一,有6個頂點和12條邊。正八面體展開圖呈現了它的幾何結構,並提供了對其形狀和特徵的深入理解。透過正八面體展開圖,我們可以探索這種充滿幾何美的立體形狀。」
正八面體
一個正八面體是一種由八個等邊三角形構成的立體幾何圖形,這些三角形分為上、下兩層,每層四個,通過將一個正方形各邊的中點連接起來形成。這樣組成的結構看起來像是一個正方錐體,上下兩部分通過這些三角形邊相連接。正八面體是五種正多面體之一,另外四種是正四面體、正六面體、正十面體和正十二面體。


結構特徵
正八面體具有幾個顯著的特徵:
- 頂點數目: 6個。
- 邊數目: 12條邊。
- 面數目: 8個面,都是等邊三角形。
- 對稱性: 正八面體具有八重對稱性,即旋轉結構的任意一個頂點周圍的基準面都可以使它回到原來的位置。
- 正三角形反稜柱: 正八面體可以被視為一個正三角反稜柱,因為它的對面是兩組相對的等腰三角形。
應用
正八面體在自然界和人工結構中都有出現。在自然界中,一些礦物如輝石和金綠玉的晶體結構就是正八面體的形狀。在人工結構中,正八面體可以用於建築設計、藝術裝置,甚至是遊戲設計(如骰子)。
正八面體作為一種美麗而對稱的幾何形體,不僅具有科學上的意義,也是數學美學的一個體現。
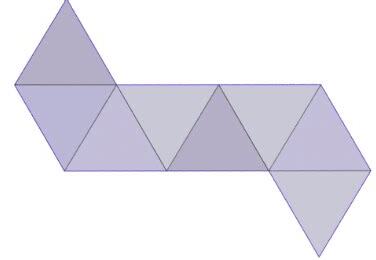
正八面體展開圖是一種幾何圖形,具有八個相等的正等邊三角形面。它是一種多面體,每個面都連接著其他三個面,形成八個面都相交的構造。
正八面體展開圖以其獨特的形狀和結構而聞名。它可以被視為正四面體的展開圖,其中每個面都被剖成多個三角形,再展開成二維圖形。這樣的展開圖使我們可以更好地理解和研究正八面體的性質和特徵。
正八面體展開圖可以用來探索多個科學和數學概念。例如,在計算幾何中,它可以幫助我們計算正八面體的面積和體積。在拓撲學中,它可以被用來研究多面體的拓撲特點,例如歐拉公式。
該展開圖也可以作為藝術品的靈感來源。許多藝術家利用正八面體展開圖的幾何美感和對稱性創作獨特的作品。藝術家可以通過將不同的顏色和圖案應用到每個三角形面上,來創造出令人驚嘆的視覺效果。
此外,正八面體展開圖還在遊戲設計和建築中有廣泛的應用。在遊戲中,它可以被用作多面骰子,每個面代表一個數字或符號。在建築中,它可以被用來設計獨特的建築結構,並提供強大的支撐能力。
總結來説,正八面體展開圖是一種重要的幾何圖形,具有著廣泛的應用領域。不僅可以用於科學和數學研究,還可以成為藝術和遊戲的靈感來源。它的獨特形狀和結構令人著迷,對於探索和理解多面體的特性至關重要。
延伸閲讀…
正多面體
正八面體- 維基百科,自由的百科全書
