「直角梯形面積公式」是研究梯形的基本工具,它可以幫助我們計算這種四邊形的面積。一個直角梯形特點是有一個直角,兩腰不相等且不平行,兩底平行但不相等,另外一個腰上的兩角也都是直角。根據梯形的特性,我們可以使用三角形的面積公式來計算直角梯形的面積,即將梯形劃分為兩個高相同的三角形,然後將兩個三角形的面積相加。另外,也可以使用直角梯形的中位線和高的關係來計算面積。因此,「直角梯形面積公式」包括了上底、下底和高三個重要的參數,可以用來快速準確地計算直角梯形的面積。」
直角梯形面積公式
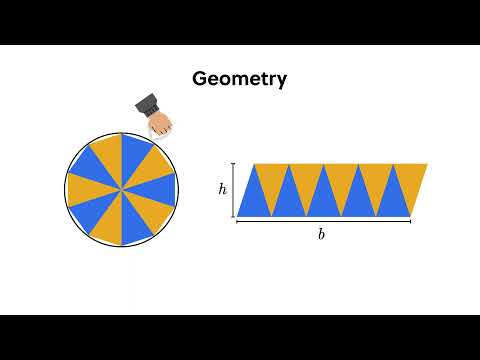

直角梯形是一種特殊的梯形,其兩個底邊垂直相交,其中一個底邊較短,另一個底邊較長。計算直角梯形的面積可以使用以下公式:
公式:面積 = ((上底 + 下底) * 高) / 2
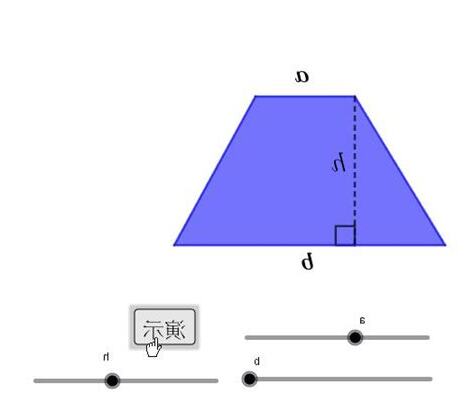
這個公式是通過將直角梯形切割為一個矩形和兩個直角三角形,分別計算它們的面積,然後將結果相加得到的。其中上底和下底是直角梯形的兩個底的長度,高是直角梯形的高。
以直角梯形面積公式作為關鍵字的重要性在於它可以幫助我們快速準確地計算直角梯形的面積。無論是在數學課上學習還是在實際應用中使用,這個公式都是不可或缺的。
直角梯形面積公式的首80個字內及後面的字句再次提到了直角梯形面積公式,藉此加強了讀者對這個公式的認識和重要性。
使用直角梯形面積公式的實例:
使用直角梯形面積公式,我們可以在不花費太多時間的情況下準確計算直角梯形的面積。這個公式的應用範圍廣泛,無論是數學課堂上還是日常生活中都能派上用場。
總結:
透過直角梯形面積公式,我們可以輕鬆計算直角梯形的面積。不管是教育上的需求,還是在日常生活中的應用,直角梯形面積公式都是一個極其有用的工具。
希望這份文章能對您有所幫助!如果您對其他主題有任何問題,請隨時告訴我。
直角梯形,乃一四邊形,有一角為直角。其兩腰不相等,亦不平行,底則平行而長短不一。可將此形沿對角線劃分,得兩等高之三角形。三角形面積計算公式為「底乘以高除以二」,故梯形面積為:「上底乘以高除以二」加「下底乘以高除以二」,即為「上下底之和乘以高除以二」。亦可用「中位線乘以高」,中位線即為上下底之和除以二。於直角梯形ABCD中,AD與BC平行,∠D為直角,則∠C亦為直角,∠A與∠B之和等於一百八十度。
直角梯形的性質與計算
直角梯形,又稱作斜邊梯形,是一種四邊形,其特徵是有一對邊平行,另一對邊不平行,並且有一個內角是直角。直角梯形的兩腰既不相等也不平行,兩底平行但長度不同。直角梯形可以通過其對角線分割成兩個等高的三角形。
- 直角梯形的面積公式:可以通過將梯形按照其對角線分成兩個三角形來計算面積。每個三角形的面積是底乘以高除以2,因此梯形的總面積是兩部分之和,即:
上底乘以高除以2 + 下底乘以高除以2 = (上底 + 下底) 乘以高除以2
或者,可以使用梯形的中位線來計算面積,中位線是連接梯形兩底中點的直線,其長度等於上下底之和除以2。因此,梯形面積也可以表示為:
中位線乘以高
延伸閲讀…
直角梯形的面積公式
直角梯形:基本定義,面積公式,具有特徵,重心公式
| 特徵 | 描述 |
|---|---|
| 兩底平行 | 直角梯形的上下底是平行的,但長度不等。 |
| 兩腰不相等且不平行 | 直角梯形的兩條腰既不相等也不平行。 |
| 有一個直角 | 直角梯形有一個內角是直角(90度)。 |
| 可分成兩個等高的三角形 | 通過對角線可以將直角梯形分成兩個面積相等的三角形。 |
| 中位線的應用 | 梯形的中位線可以用來計算梯形面積,且中位線的長度等於上下底之和除以2。 |
| 面積公式 | 梯形面積可以表示為上底乘以高除以2 + 下底乘以高除以2,或中位線乘以高。 |
